
In practice, however, most oil immersion objectives have a maximum numerical aperture of 1.4, with the most common numerical apertures ranging from 1.0 to 1.35. By examining the numerical aperture equation above, we find that the highest theoretical numerical aperture obtainable with immersion oil is 1.51 (when sin ( m) = 1). Most objectives in the magnification range between 60x and 100x (and higher) are designed for use with immersion oil.
You should check with the manufacturer if there are any doubts. We suggest that microscopists never use objectives designed for oil immersion with either glycerin or water, although several newer objectives have recently been introduced that will work with multiple media. Care should be used with these objectives to prevent unwanted artifacts that will arise when an objective is used with a different immersion medium than it was designed for. Microscope objectives are now available that allow imaging in alternative media such as water (refractive index = 1.33), glycerin (refractive index = 1.47), and immersion oil (refractive index = 1.51). Therefore, in order to obtain higher working numerical apertures, the refractive index of the medium between the front lens of the objective and the specimen must be increased. As the light cones change, the angle m increases from 7° in Figure 2(a) to 60° in Figure 2(c), with a resulting increase in the numerical aperture from 0.12 to 0.87, nearing the limit when air is the imaging medium.īy examining the numerical aperture equation, it is apparent that refractive index is the limiting factor in achieving numerical apertures greater than 1.0.
#Angular resolution calculator series
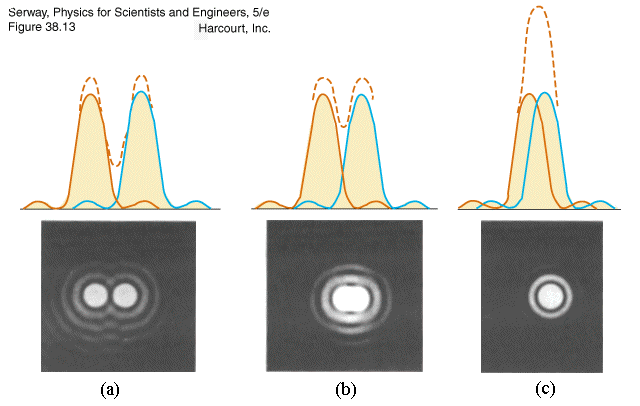
Figure 2 illustrates a series of light cones derived from objectives of varying focal length and numerical aperture. In practice, however, it is difficult to achieve numerical aperture values above 0.95 with dry objectives. Higher numerical apertures allow increasingly oblique rays to enter the objective front lens, producing a more highly resolved image. Numerical Aperture Light Cones Explore how the size and angular aperture of the light cone captured by a microscope objective changes with numerical aperture. The sin of the angle m, therefore, has a maximum value of 1.0 (sin(90°) = 1), which is the theoretical maximum numerical aperture of a lens operating with air as the imaging medium (using "dry" microscope objectives). From this equation it is obvious that when the imaging medium is air (with a refractive index, n = 1.0), then the numerical aperture is dependent only upon the angle m whose maximum value is 90°. Many authors substitute the variable a for m in the numerical aperture equation. Where n is the refractive index of the imaging medium between the front lens of the objective and the specimen cover glass, a value that ranges from 1.00 for air to 1.51 for specialized immersion oils. The angle m is one-half the angular aperture ( A) and is related to the numerical aperture through the following equation : Numerical Aperture ( NA) = n(sin m)

A longitudinal slice of this cone of light shows the angular aperture, a value that is determined by the focal length of the objective. Image-forming light waves pass through the specimen and enter the objective in an inverted cone as illustrated in Figure 1. The numerical aperture of a microscope objective is a measure of its ability to gather light and resolve fine specimen detail at a fixed object distance. Microscope Objectives Numerical Aperture and Resolution

Molecular Expressions Microscopy Primer: Anatomy of the Microscope - Numerical Aperture and Resolution


 0 kommentar(er)
0 kommentar(er)
